冒泡，二分，合并，快速排序

二分排序法

二分查找法主要是解决在“一堆数中找出指定的数”这类问题。

而想要应用二分查找法，这“一堆数”必须有以下特征：

  1. 存储在数组中
  2. 有序排列

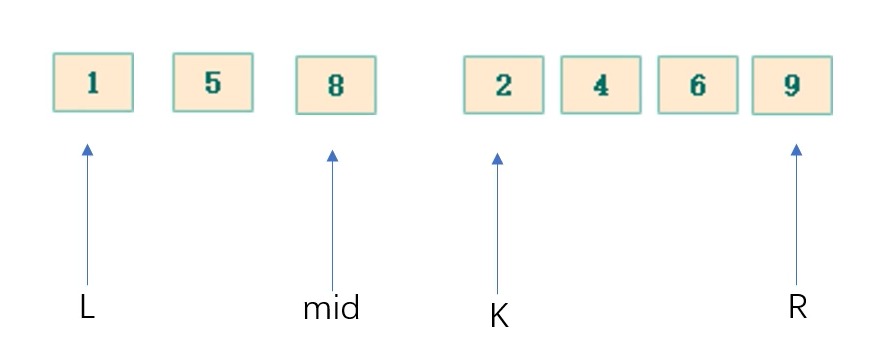
二分查找思路，在一个有序的数组中（从小到大排列），与中间的那个数作比较，若相等，则找到，若小于中间的数则继续在左边那一块重复操作，反之重复右边的那块操作。

有递归方法与普通方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import java.util.Arrays;
import java.util.Scanner;

/**
 * 输入一个int n表示有几个数 接着输入n个有序的数字即可
 * 
 * @author 煨酒小童
 *
 */
public class BinarySearch0 {
	static int haha = 7; // 查找7这个数的下标

	public static void main(String[] args) {
		Scanner in = new Scanner(System.in);
		int n = in.nextInt();
		int num[] = new int[n];
		for (int i = 0; i < n; i++)
			num[i] = in.nextInt();
		Arrays.sort(num); // 排为有序
		in.close();
		System.out.println(find(num, 0, n - 1));
	}

	// i为左边界，j为右边界
	// 非递归方式
//	private static int  find(int[] num, int i, int j) {
//		while(i<=j) {
//			int mid=(i+j)/2;
//			if(num[mid]==haha)
//				return mid;
//			else if(num[mid]>haha)
//				j=mid-1;
//			else
//				i=mid+1;
//		}	
//		return -1;
//		
//	}
	// 递归方式
	private static int find(int[] num, int i, int j) {
		int mid = (i + j) / 2;
		if (i > j)
			return -1;
		else if (num[mid] == haha)
			return mid;
		else if (num[mid] > haha)
			return find(num, i, mid - 1);
		else
			return find(num, mid + 1, j);

	}
}

合并排序

采用分治的思想层层剖析再合并

思路：把一个数组分成两半，分别排好序，然后再合并一个完整的有序的数组（他的优点在于对于已排好序的两部分进行合并非常精妙且快速），在分成两半后，它还可以进行再分两半，直到分的不能再分为止。一直分分分，就是分治法的精髓。
merge方法也就是合并是难点所在：

本质是 L 与 K 的比较，谁大（或小）就把所指的数放入 temp 数组中，并把指针移动到下一位，一直重复下去，当有一方越过其自己的边界，意味着另一方还有剩余，则把剩余的全部放在 temp 数组中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
public class MergeSort {
	static int num[];

	public static void main(String[] args) {
		int n = 20;
		num = new int[n];
		for (int i = 0; i < n; i++) {
			double d = Math.random();
			num[i] = (int) (d * 100);
			System.out.print(num[i] + " ");
		}
		// 上面生成20个0-100的随机数
		mergesort(num, 0, n - 1); // 合并排序
		System.out.println();
		for (int i : num)
			System.out.print(i + " ");
	}

	private static void mergesort(int[] num2, int left, int right) {
		if (left < right) {
			int mid = (left + right) / 2;
			mergesort(num2, left, mid);
			mergesort(num2, mid + 1, right); // 这里利用了递归与分治
			merge(num2, left, right);
		}

	}

	private static void merge(int[] num2, int left, int right) {
		int k = 0, mid = (left + right) / 2, left0 = left, // 这个暂时不思考，看到后面就理解了
				j = mid + 1, // 另一半的左边的下标
				temp[] = new int[(right - left) + 1]; // 装排好序的数
		while (left <= mid && j <= right) {
			if (num2[left] < num2[j])
				temp[k++] = num2[left++];
			else
				temp[k++] = num2[j++];
		}
		if (left > mid) // 第二个序列有剩余，则把剩余的数依次写在temp后面
			for (int i = j; i <= right; i++)
				temp[k++] = num2[i];
		if (j > right)
			for (int i = left; i <= mid; i++)
				temp[k++] = num2[i];
		for (int i = 0; i < temp.length; i++)
			// 这里一定要是left0，深处想想复制进入原数组，其他位置不能改动，假如left=3，right=8，则复制进去的时候还是从3到8
			num2[left0++] = temp[i];

	}

}

参考视频

快速排序


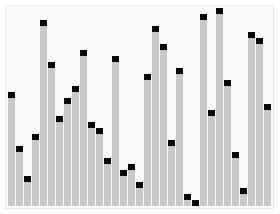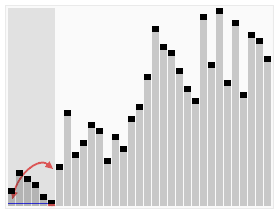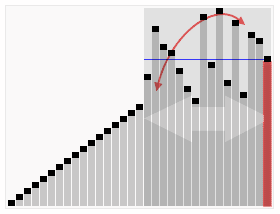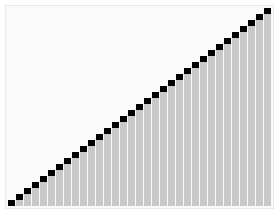
快速排序是冒泡排序的改进版，思路是，在其中找一个基准值，然后比较这个基准值，把整个数组分成都比基准值大的一部分，和都比他小的一部分，然后对剩下的两大部分，又可以进行类似操作。（对于基准值分成两大部分的函数最为妙，边界条件很不好理解，我要背下来！！太妙了)因为排序是就地进行的，不像合并排序一般还要再誊一遍值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import java.util.Scanner;

public class QuickSort {

	public static void main(String[] args) {
		int n = 8;
		int num[] = new int[n];
		Scanner in = new Scanner(System.in);
		for (int i = 0; i < n; i++) {
			double d = Math.random();
			num[i] = (int) (d * 100);
			System.out.print(num[i] + " ");
			// num[i]=in.nextInt();
		}
		// 以上为随机生成8个数
		qSort(num, 0, n - 1);
		System.out.println();
		for (int i : num)
			System.out.print(i + " ");

	}

	private static void qSort(int[] num, int i, int j) {
		if (i < j) {
			int q = partion(num, i, j);
			// 下面不要包含q了，q算一个中间值独立存在,只用再考虑两边就行了
			qSort(num, i, q - 1); // 有分治的思想
			qSort(num, q + 1, j);
		}

	}

	private static int partion(int[] num, int i, int j) {
		int bid = num[i];
		int haha = i, k = j + 1;
		while (true) {
			while (num[++i] < bid && i < j)
				; // 寻找比bid大的那个数，找到并暂停
			while (num[--k] > bid && k >= i)
				; // 寻找比bid小的那个数,找到并暂停，这里为什么可以不用写k>=i?? 惊呆我了
			if (i >= k)		//如果没有遍历完，则进行上面两个值的交换
				break;
			// 交换
			int temp = num[i];
			num[i] = num[k];
			num[k] = temp;
		}
		num[haha] = num[k];
		num[k] = bid;
		return k;

	}

}

参考视频

冒泡排序

最好情况时间复杂度为O(n),最差为O(n^2)

如 7， 3， 9 ，2， 5

  1. 3 7 2 5 9
  2. 3 2 5 7 9
  3. 2 3 5 7 9
  4. 2 3 5 7 9
  5. 2 3 5 7 9

其实冒泡的本质是：有几个数就重复几趟，每一趟中都依次两两递进扫描，若不符合位置的则交换，每一趟下来都会找到一个最大值放在后面，所以后面扫描的时候可以跳过这个最大值少少扫描一点。

数组 a 中装着乱序的数

1
2
3
4
5
6
7
8
9
for(int i=0;i<a.length;i++) {          //进行n趟
	for(int j=0;j<a.length-1-i;j++) {       //两两递进扫描
		if(a[j]>a[j+1]) {
			int temp=a[j];
			a[j]=a[j+1];
			a[j+1]=temp;
		}
	}
}
#java #算法
冒泡，二分，合并，快速排序
https://lililib.github.io/冒泡，二分，合并，快速排序/
作者
煨酒小童
发布于
2020年12月19日
许可协议