哈夫曼编码

构造哈夫曼树时使用双亲孩子的存储结构，需要数据有： 权重，他们母亲是谁，是否加入了哈夫曼树，他们左孩子与右孩子又是谁？

步骤：

  1. 单节点的初始化入哈夫曼树中，初始化2*n-1个节点
  2. 寻找两个权重最小且还没有加入树中的节点进行构造哈夫曼树，不断重复此过程（构造过程中存储结构中变动的信息都需要更新）其实这寻找两个权值最小的节点挺难的，困了好长时间/(ㄒoㄒ)/~~
  3. 根据构造的树，解析析出哈夫曼编码

双亲孩子节点


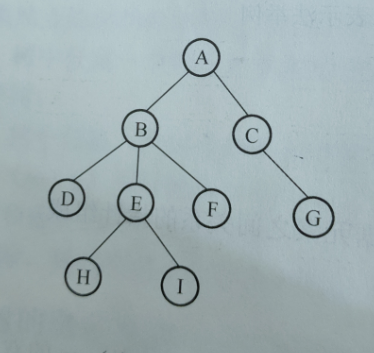
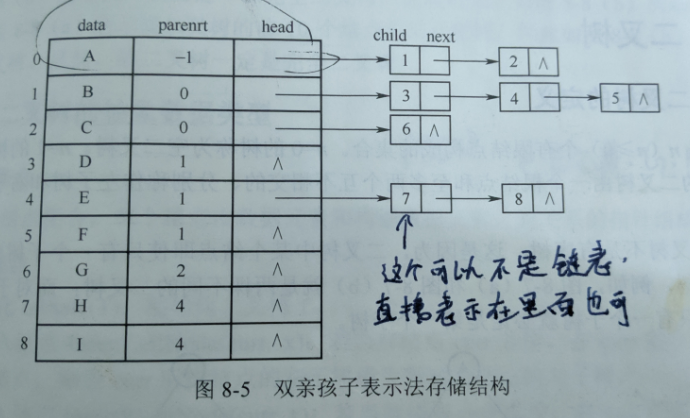
上图把head换成leftchild 和 rightchild就可以代表仿真指针实现的双亲孩子的储存结构

  get了一个新技巧，对于一个数组中胡乱的加入各个大小的数据，怎么循环一次就可以把其中最小的和次小的下标找到,分两个情况考虑：

  1. 最小值在次小值右边，想象着最小值在最右边，一直遍历下去定会也遇到次小值
  2. 最小值在次小值左边，
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
    int big1=9999,
	big2=9999,
	index1 = 0,
	index2 = 0;
//找出权值最小和次小的树
for(int j=0;j<n+i;j++) {
	if(big1>tree[j].weight && tree[j].flag==0) {//这个是最小值在次小值右边
		big2=big1;
		index2=index1;		
		big1=tree[j].weight;
		index1=j;		//smallest
	}	
	else if(big2>tree[j].weight && tree[j].flag==0 ) {//最小值在次小值左边
		big2=tree[j].weight;
		index2=j;		//second smallest
		
	}
}

源码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
import java.util.ArrayList;

public class HuffmanCoding {
	static int weight[]=new int[] {1,3,5,7};
	public static void main(String[] args) {
		hufftree tree[]=new hufftree[weight.length*2-1];
		for(int i=0;i<tree.length;i++)
			tree[i]=new hufftree();
		haffman(weight,tree);
		huffcode code[]=new huffcode[weight.length];
		for(int i=0;i<weight.length;i++)
			code[i]=new huffcode();
		generateHuffCode(tree,code);
		//输出哈夫曼码
		for(int i=0;i<code.length;i++) {
			ArrayList<Integer> a=code[i].code;
			String s="";
			for(int j=a.size()-1;j>=0;j--) {
				s+=a.get(j);
			}
			System.out.println(code[i].weight+"  :"+s);
		}
		System.out.println(123);
	}
	
	//哈夫曼码的生成
	private static void generateHuffCode(hufftree[] tree, huffcode[] code) {
		
		for(int i=0;i<code.length;i++) {
			int parents=tree[i].parents;
			int child=i;
			int weight=tree[i].weight;
			code[i].weight=weight;
			while(parents!=-1) {		//这里是把结果倒过来保存
				if(tree[parents].leftchild==child)
					code[i].code.add(0);		
				else
					code[i].code.add(1);
				child=parents;			//妙哉
				parents=tree[child].parents;
			}
		}
		
	}

//哈夫曼树的构建
	static void haffman(int weight[],hufftree tree[]) {
		int n=weight.length;
		//哈夫曼树的初始化，共有2*n-1个节点
		for(int i=0;i<tree.length;i++) {
			if(i<n) tree[i].weight=weight[i];
			else 	tree[i].weight=0;
			tree[i].flag=0;
			tree[i].parents=-1;
			tree[i].leftchild=-1;
			tree[i].rightchild=-1;
		}
		//构造非叶子节点，2*n-1-n个
		for(int i=0;i<n-1;i++) {
			int big1=9999,
				big2=9999,
				index1 = 0,
				index2 = 0;
			//找出权值最小和次小的树
			for(int j=0;j<n+i;j++) {
				if(big1>tree[j].weight && tree[j].flag==0) {//这个是最小值在次小值右边
					big2=big1;
					index2=index1;		
					big1=tree[j].weight;
					index1=j;		//smallest
				}	
				else if(big2>tree[j].weight && tree[j].flag==0 ) {//最小值在次小值左边
					big2=tree[j].weight;
					index2=j;		//second smallest
					
				}
			}
			tree[index1].parents=n+i;//这里是从i=0开始的
			tree[index2].parents=n+i;
			tree[index1].flag=1;
			tree[index2].flag=1;
			tree[n+i].weight=tree[index1].weight+tree[index2].weight;
			tree[n+i].leftchild=index1;
			tree[n+i].rightchild=index2;
			}
		}
	}
class huffcode{
	ArrayList<Integer> code=new ArrayList<Integer>();
	int weight;
}


class hufftree{
	int weight,
		flag,			//是否已经加入到哈夫曼树中，1为已加入
		parents,
		leftchild,
		rightchild;
}

#java #算法
哈夫曼编码
https://lililib.github.io/哈夫曼编码/
作者
煨酒小童
发布于
2020年12月20日
许可协议