图的着色问题（地图着色问题）

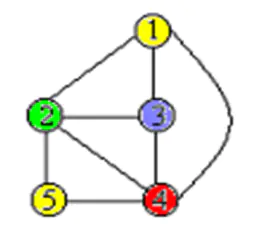
问题描述

   给定无向连通图G=(V, E)和m种不同的颜色，用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中相邻的两个顶点有不同的颜色?
   这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的两个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。
   编程计算：给定图G=(V, E)和m种不同的颜色，找出所有不同的着色法和着色总数。
简而言之：给一个图，要求相连接的顶点颜色不能相同，有m种颜色可以进行着色，可以有多少方案。

思路

  可以想第一个顶点第一种颜色，第二个点再尝试每个颜色是否可以着色，以此类推，有递归的感觉。
  如同八皇后问题，放置顶点，循环尝试其中一个颜色（ 颜色方案存入其中名为 x 的数组中），然后检查颜色是否合法（不与任何相连的顶点颜色相同为合法），如果不合法，回溯重试颜色，如果合法，就放置下一个顶点，直到所有顶点放置完毕，则为一成功方案。

源码

public class mapColoring {
	static int n = 5; // 有n个结点
	static int[] x = new int[n + 1]; // answer pace 按顶点1，2，3，4，5，6对应的颜色
	static int m = 4; // 可用颜色数
	static int[][] map = new int[n + 1][n + 1];
	static int sum = 0;

	public static void main(String[] args) {
		initial(map);
		backtrack(1);
		System.out.println(sum);
	}

	private static void backtrack(int t) {
		if (t > n) {
			sum++;
			for (int i = 1; i <= n; i++) {
				System.out.print(x[i] + "  ");
			}
			System.out.println();
			return;// ?????
		} else {
			for (int i = 1; i <= m; i++) {
				x[t] = i; // 顶点t被予以第i中颜色
				if (check(t))// 这里包含了剪枝
					backtrack(t + 1);
				x[t] = 0;// 如果颜色不行，回溯回去

			}
		}

	}

	private static boolean check(int t) {
		for (int j = 1; j <= n; j++) {
			if (map[t][j] == 1 && x[t] == x[j])
				return false;
		}
		return true;
	}

	/**
	 * 为1是相连，否之为0
	 * 
	 * @param map
	 */
	private static void initial(int[][] map) {
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				map[i][j] = 1;
				if (i == j)
					map[i][j] = 0;
			}
		}
		map[1][5] = 0;
		map[5][1] = 0;
		map[3][5] = 0;
		map[5][3] = 0;

	}
}

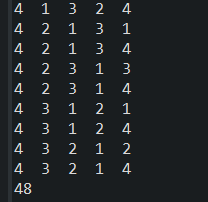
运行截图