
0-1背包问题:假设你是个小偷,背着一个可装4磅东西的背包。你可盗窃的商品有如下3件

为了让盗窃的商品价值最高,你该选择哪些商品?
每个动态规划算法都从一个网格开始,背包问题的网格如下:
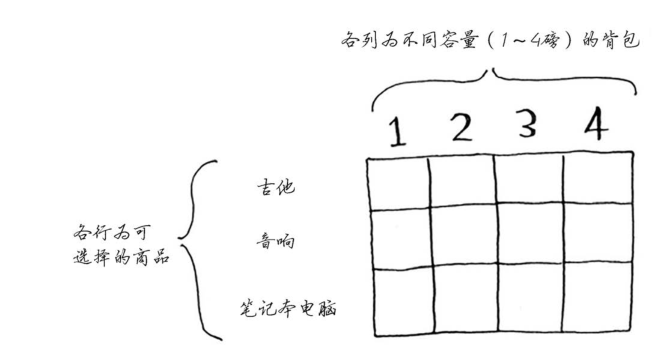
网格的各行为商品,各列为不同容量(1~4磅)的背包。所有这些列你都需要,因为它们将
帮助你计算子背包的价值。
网格最初是空的。你将填充其中的每个单元格,网格填满后,就找到了问题的答案
一行一行的填值,想象一个货架一个货架的取,还没有走到的货架不能取(可以回头),从左往右的每一列背包空间变大
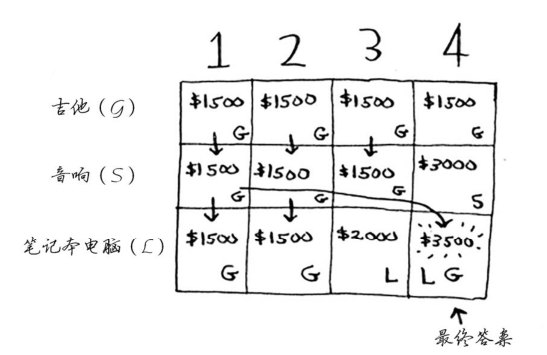
计算每个单元格使用了如下公式:

优化: 因为看表或通过公式可以发现,下一行的数据只与上一行的数据有关,所以可以弄一个一维数组,通过刷新模拟换行填数据,需要注意的是,从后往前填,因为正过来填的话,后面要填的值可能是与被修改的值有关
练习

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
public class Knapsack0_1_Problem {
public static void main(String[] args) {
int weight = 6;
int wei[] = new int[] { 0, 3, 1, 2, 2, 1 };
int value[] = new int[] { 0, 10, 3, 9, 5, 6 };
int map[][] = new int[wei.length + 1][weight + 1];
int map1[] = new int[weight + 1];
for (int i = 1; i <= value.length - 1; i++) {
for (int j = map1.length - 1; j >= 1; j--) {
if (j >= wei[i]) {
map1[j] = Math.max(map1[j], value[i] + map1[j - wei[i]]);
}
}
}
for (int i : map1) {
System.out.println(i);
}
}
}
|
参考书籍





